力学の世界で、回転を表す定義で一般的なのは以下の３つです。

Ｎ：力のモーメント（トルク） Ｆ：ベクトル ｒ：位置ベクトル（ここではヨーヨーの半径に相当） Ｌ：角運動量 ｐ：運動量 Ｉ：慣性モーメント ｍ：物体の質量

力のモーメントとは、てこの原理です。

（力のモーメント）＝（回転半径）×（回転させる向きに働く力）

てこの原理 (Fig.1) では、支点の位置によって、物体を動かすために必要な力が変わってきます。物体を動かすための力を小さくしたい場合は、力点を支点からなるべく離す必要があります。

てこの原理に関連して、ヨーヨーに関する身近な例を考えてみましょう。カウンターウエイトスタイルに最適なヨーヨーのひとつ『フリーハンド』で、ウエイト（重り）として使われるプラスチックダイスの重さは11グラム、ヨーヨー本体は64グラムです。プロペラ（ヨーヨートリックの一種）を行うとき (Fig.2) 、力のモーメントのバランスが取れる支点の距離を計算してみましょう。

筆者の身長で、へそ下で糸の長さを調節すると、糸の長さは85センチでした。その場合、指からヨーヨーの長さが12.5センチが、最もバランスの取りやすいポイントになります。

これは、ヨーヨーのウエイトバランスにも当てはまります。

ヨーヨーの軸は中心を通っています (Fig.3) 。これは当然のことですが、重量配分が違っていたらどうなるでしょうか。

左右に１：２の重りを配置した場合、中心に軸が通っていたら力のモーメントのバランスが悪く、すぐ回転が止まってしまいます (Fig.4) 。重いほうがどんなに回ろうとしても、軽いほうが足を引っ張るので、回転はどんどん落ちていきます。効率よく回転を続けさせるためには、力のモーメントを左右同じにする必要があります。

中心位置をずらしてやると、力のモーメントは釣り合うため、安定して回転することができます (Fig.5) 。

ヨーヨーの回転運動にも、こういった物理が影響していることがおわかりいただけたでしょうか？

まず、慣性モーメントについて確認してみましょう。角運動量（ヨーヨーに与えられる回転のための力）は半径×運動量です。運動量は質量×速度で、速度は角速度×半径で表せます。

これより、角運動量Ｌと慣性モーメントの関係は、以下のようにして表すことができます。

Ｌ：角運動量 ｒ：位置ベクトル（ここではヨーヨーの半径に相当） ｐ：運動量 ｖ：速度 ｍ：物体の質量 ω：角速度（ヨーヨーの回転速度）

運動量に相当する角運動量Ｌと、速度に相当する角速度ωを定義すると、運動量の定義である

と同じように、

　　（Ｉ：慣性モーメント）

と表すことができます。

この回転と質量の相関を表す量であるＩが慣性モーメントです。質量が「動きやすさ」「止まりやすさ」を表すのと同様に、慣性モーメントＩは「回しにくさ」「止まりにくさ」を表す値となります。

角運動量Ｌが同じであれば、半径ｒが小さくなればなるほど、運動量ｐが大きくなります。

ｐ（運動量）＝ｍ（重質量）ｖ（速度）なので、

となります。

同じ角運動量Ｌで回ってる物体は、ヨーヨー半径ｒが小さいほど、運動量ｐが大きくなります。これはフィギュアスケートのスピンで、腕を狭めると回転速度が上がるのと同じ理屈です。

慣性モーメントＩは、回しにくさを指します。

であることを考えると、半径ｒが大きくなるとＩも大きくなって回転しにくくなり、半径ｒが小さいとＩも小さくなって回転しやすくなります。式を見ると、半径ｒがかなり優位な位置を占めていることが分かります。

以上より、一般に「半径が大きく重いヨーヨーは回転力を稼ぎやすい」と思われがちですが、慣性モーメントを考えると、

・慣性モーメントの小さい（半径が小さく軽い）ヨーヨーは回転させやすい

・慣性モーメントの大きい（半径が大きく思い）ヨーヨーは回転させにくい

ということが分かります。

回転体の持つエネルギーＫは、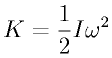

（回転体の持つエネルギー）＝1/2×（質量×半径の２乗×角速度の２乗）

運動エネルギーは、中学でも習っているはずです。よって、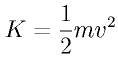

と同義です。これに傾きに対するcosθを乗ずることでジャイロ効果の力が分かります。

ジャイロ効果

（θ：傾き角度）

ちなみに、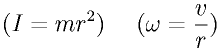

速度に換算することでｒが消えるため、高校で学習する運動エネルギーと同じ

となります。

・慣性モーメントを小さくして（回りやすくして）回転数を稼ぐ

・慣性モーメントを大きくし、強大な力を持って投げ下ろすことで充分なパワーを与える

物体が持つ回転数（回転力）は、力さえかければ無限に増えていきます。しかし、人間が投げる以上、かけられる力には限界があります。投げ下ろしの力に合った慣性モーメントのヨーヨーでないと、十分な回転数を得ることはできません。

ですが、これを言い換えてみると、大きな慣性モーメントを持ったヨーヨーをスーパーサイヤ人のような規格外の力で投げ下ろしたら、強力な回転を生み出すことができるのではないでしょうか？

結局のところ、自分の力にあったヨーヨーを使うのが寛容です。重くて大きいヨーヨーを使おうにも、回転をかけにくいのであればどうしようもありません。

半径を大きくした場合と、重量を増やしていった場合の角運動量（投げ下ろした力がヨーヨーに伝わる力）を比べてみましょう（他の条件は同じとします）。

同じ力で投げた場合、重量を増やすよりも、半径を大きくしたほうが回転（角運動量)がつけやすいのです。極端な例ですが、半径を10倍した場合と重量を10倍した場合を比べると、同じ１０倍でも回転数が１０と１００、というように１０倍の開きになります。１５倍だとおよそ２０倍、２０倍だと４０倍近くに…といった具合です。

それでは、同じ力で投げ下ろした場合はどうなるでしょうか？

重量を変化させた場合は回転数が1/2に、半径を２倍にした場合は回転数が1/4になります。

とはいえ、ここまで述べた式は、ヨーヨーの質量配分を考慮していません。

シングルハンドストリングプレイ用の高級機には、たいてい金属リムと呼ばれる、真鍮・アルミなど金属製のリングが取り付けられており (Fig.8) 、重量配分が外側に大きく偏っています。重量配分のせいで、実際の半径と理論上の半径が大きく異なってくるのです。

それ以外でも、プラスチック製・金属製・木製など、様々な材質のヨーヨーが存在しており、重量配分もそれぞれ異なります。ですが、重量配分の似ている、プラスチック製機種同士、金属リム機種同士であれば参考になるでしょう。

ヨーヨーは、慣性モーメントが小さい方が良く回ります。慣性モーメントは重量より半径の効果が大きいです。

・車のホイールは、軽量なアルミホイールの方が良い（重量を軽く）

・車のタイヤは、インチサイズを小さくすると加速が良い（半径を小さく）

・野球やゴルフのスイングは、脇を締めると良い（半径が小さくなることでスイングスピードが上がる）